Trigonometry¶
Surprisingly we still hear many tease and joke about trigonometry, generally in the vain of being nerdy or complicated. Take away the self imposed avoidance and we find that trigonometry is the relation of mathmatic coordinates and the real world.
PI (π)¶
PI will be the central point of a lot of trigonometry. So many things in the world are in PI ratio to something else. Primarily the diameter of a circle to its circumference. However lets not go into history lessons until it becomes more interesting.
Note
PI is irrational, so there is no exact value. However we can easily get well over the accuracy needed for anything within reason.
Note
3.1415926535897932384626433832795
Note
Fraction approximations: 22/7, 333/106, 355/113, 52163/16604
Radians and Degrees¶
Lets do a 360. Or we are 180º out of wack?
Radians don’t make any sense do they? We all know 360º. Trigonometry is known from making use of triangles with one angle that is 90º. So why the weird radians?
Actually our 360º is the aproximate preschool version of angles before useful numbers were invented. Aprox 4500 years, Sumerians and Egyptians based the units of a circle off of how they divided up a year. They got it a little wrong, but had noticed the movement of the sun and stars on a 360 day cycle. Seemed good enough and did the trick, so they began using that as a division base. Circles in 360 divisions became the basis of our “degrees” system.
So mathmatically, 360º is useless. You really would never need to be in degrees. But since it is the most recognizable, we need to know how to convert back and forth for sanities sake.
Note
π/180 = 0.01745329251994329576923690768489
Note
90º * (π/180) = 1.57079632
Note
1.57079632 / (π/180) = 90º
Tip
Only convert back out to degree when ready to display for human readability
The above can come in useful if the script or languange you are writing in doesn’t have a rad to deg to rad function. Don’t be afraid to use it, it is a very simple calculation.
Right Angles¶
Find your right angle! Figuring the calculations will just be the math later. But identifying where your right angles are can be the creative part. This image for example came up when figuring out how to calculate how much to turn in order to avoid an obstacle. We have our subject’s position, the position of the object and how wide it is.
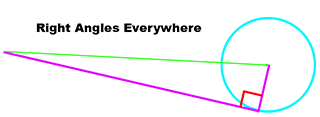
The edge of the radius’ would be it’s tangent, which is what do not have. Just so happens that its tangent would be where the right angle would be. Now you have enough information to figure anything out.